Եռանկյուններ

Եռանկյուններ

Եռանկյունը կազմված է միևնույն ուղղի վրա չգտնվող երեք կետերից, և այդ կետերը զույգ առ զույգ միանում են երեք հատվածների։ Այդ Կետերը կոչվում են եռանկյան գագաթներ, իսկ հատվածները՝ նրա կողմերն են։ A, B, և C գագաթներով եռանկյունը հաճախ նշանակում են ΔABC։

Եռանկյան մակերեսը հավասար է նրա հիմքին որը բարձրության արտադրյալի կեսին է:

երեք կողմերի երկարությունների գումարը եռանկյան պարագիծ է կոչվում:

Եռանկյան տեսակներ[խմբագրել | խմբագրել կոդը]

Կախված կողմերի երկարությունների փոխհարաբերությունից և անկյունների մեծությունից, եռանկյունները լինում են ուղղանկյուն (անկյուններից մեկն ուղիղ է), բութանկյուն (անկյուններից մեկը բութ է), սուրանկյուն (բոլոր երեք անկյունները սուր են),

Ուղղանկյուն	Բութանկյուն	Սուրանկյուն

հավասարակողմ կամ կանոնավոր (բոլոր երեք կողմերն իրար հավասար են) և հավասարասրուն (հավասար են գոնե երկու կողմերը)։

Հավասարակողմ	Հավասարասրուն

Եռանկյունների հավասարություն և նմանություն[խմբագրել | խմբագրել կոդը]

Եռանկյունների հավասարություն[խմբագրել | խմբագրել կոդը]

Եռանկյունները հավասար են, եթե հավասար են նրանց համապատասխան կողմերն ու համապատասխան անկյունները։

Եռանկյունների հավասարության հայտանիշները՝

• Եթե մի եռանկյան երկու կողմերը և նրանցով կազմված անկյունը համապատասխանաբար հավասար են մյուս եռանկյան երկու կողմերին և նրանցով կազմված անկյանը, ապա այդպիսի եռանկյունները հավասար են։
• Եթե մի եռանկյան մի կողմը և նրան առընթեր անկյունները համապատասխանաբար հավասար են մյուս եռանկյան կողմին և նրան առընթեր անկյուններին, ապա այդպիսի եռանկյունները հավասար են։
• Եթե մի եռանկյան երեք կողմերը համապատասխանաբար հավասար են մյուս եռանկյան երեք կողմերին, ապա այդպիսի եռանկյունները հավասար են։

Եռանկյունների նմանություն[խմբագրել | խմբագրել կոդը]

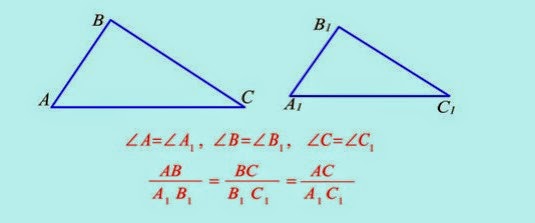
Եռանկյունները նման են, եթե այդ եռանկյունների համապատասխան անկյունները հավասար են, իսկ համապատասխան կողմերի հարաբերությունը նույնն է։ Այսինքն ∆ABC և ∆A₁B₁C₁ նման եռանկյունների միջև

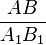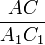 =  = , ∠A=∠A₁, ∠B=∠B₁, ∠C=∠C₁։

Եռանկյունների նմանության հիմնական թեորեմներն են՝

• Երկու եռանկյուններ նման են, եթե նրանցից մեկի երկու անկյունները համապատասխանաբար հավասար են մյուսի երկու անկյուններին։
• Երկու եռանկյուններ նման են, եթե նրանցից մեկի երկու կողմերը համեմատական են մյուսի երկու կողմերին և այդ կողմերով կազմված անկյունները հավասար են։
• Երկու եռանկյուններ նման են, եթե մեկի կողմերը համեմատական են մյուսի կողմերին։

Եռանկյան հետ կապված սահմանումներ

Եռանկյան գագաթից տարված «բարձրություն» է կոչվում այդ գագաթից նրա դիմացի կողմը պարունակող ուղղին տարված ուղղահայացը։

Ուղղանկյուն եռանկյան մեջ 30 աստիճանի դիմացի էջը հավասար է ներքնաձիգի կեսին:

Եռանկյան գագաթից տարված «կիսորդ» է կոչվում եռանկյան անկյան կիսորդի այն հատվածը, որի միացնում է այդ գագաթը և նրա դիմացի կողմի վրա գտնվող կետը։

Եռանկյան «միջնագիծ» է կոչվում այդ գագաթը և դիմացի կողմի միջնակետը միացնող հատվածը։

Եռանկյան «միջին գիծ» է կոչվում նրա երկու կողմերի միջնակետերը միացնող հատվածը։

«Ուղղանկյուն եռանկյուն» է կոչվում այն եռանկյունը, որի ներքին անկյուններից մեկը 90 աստիճան է (ուղիղ անկյուն)։ Այդ անկյան դիմացի կողմը կոչվում է «ներքնաձիգ», իսկ կից կողմերը կոչվում են ուղղանկյուն եռանկյան «էջեր»։

Ուղղանկյուն եռանկյան սուր անկյան «սինուս» է կոչվում հանդիպակաց էջի հարաբերությունը ներքնաձիգին՝

Ուղղանկյուն եռանկյան սուր անկյան «կոսինուս» է կոչվում կից էջի հարաբերությունը ներքնաձիգին՝

Ուղղանկյուն եռանկյան սուր անկյան «տանգենս» է կոչվում հանդիպակաց էջի հարաբերությունը կից էջին՝

Ուղղանկյուն եռանկյան սուր անկյան «կոտանգենս» է կոչվում կից էջի հարաբերությունը հանդիպակաց էջին՝

Մակերեսը

 Ուղղանկյուն եռանկյան մակերեսը հավասար է նրա էջերի արտադրյալի կեսին.

 Ուղղակյուն եռանկյան ուղիղ անկյան գագաթից տարված բարձրությունը

եռանկյունը բաժանում է երկու եռանկյունների, որոնցից յուրաքանչյուրը նման է

տրված եռանկյանը:

Սուր անկյան սինուսը, կոսինուսը, տանգենսը

Ուղղանկյուն եռանկյան սուր անկյան սինուս է կոչվում հանդիպակաց էջի հարաբերությունըներքնաձիգին՝

Ուղղանկյուն եռանկյան սուր անկյան կոսինուս է կոչվում կից էջի հարաբերությունըներքնաձիգին՝

Ուղղանկյուն եռանկյան սուր անկյան տանգենս է կոչվում հանդիպակաց էջի հարաբերությունը կից էջին՝

Ուղղանկյուն եռանկյան սուր անկյան կոտանգենս է կոչվում կից էջի հարաբերությունը հանդիպակաց էջին՝

Ուղղանկյուն եռանկյուն

Եռանկյունը, որի անկյուններից մեկն ուղիղ է կոչվում է ուղղանկյուն եռանկյուն:

Ուղիղ անկյան դիմացի կողմը կոչվում է ներքնաձիգ, մյուս կողմերը` էջեր:

 Ուղղանկյուն եռանկյան սուր անկյունների գումարը 90° է:

Ուղղանկյուն եռանկյան 30°-ի անկյան դիմացի էջը հավասար է ներքնաձիգի

կեսին:

 Եթե ուղղանկյուն եռանկյան էջը հավասար է ներքնաձիգի կեսին, ապա այդ էջի

դիմացի անկյունը հավասար է 30°-ի

Ներքնաձիգին տարված միջնագիծը

  Ուղղանկյուն եռանկյան ուղիղ անկյան գագաթից տարված միջնագիծը հավասար է

ներքնաձիգի կեսին:

 Եթե եռանկյան կողմին տարված միջնագիծը հավասար է այդ կողմի կեսին, ապա

այդ կողմի դիմացի անկյունը 90° է:

Հավասարության հայտանիշները

1.      Եթե մի ուղղանկյուն եռանկյան էջերը համապատասխանաբար հավասար են

մյուսի էջերին, ապա այդ եռանկյունները հավասար են:

2.      Եթե մի ուղղանկյուն եռանկյան էջը և նրան առընթեր սուր անկյունը համապա-

տասխանաբար հավասար են մյուսի էջին և նրան առընթեր սուր անկյանը, ապա

այդ եռանկյունները հավասար են:

3.      Եթե մի ուղղանկյուն եռանկյան ներքնաձիգը և նրան առընթեր սուր անկյունը

համապատասխանաբար հավասար են մյուսի ներքնաձիգին և նրան առընթեր

սուր անկյանը, ապա այդ եռանկյունները հավասար են:

4.       Եթե մի ուղղանկյուն եռանկյան ներքնաձիգը և էջը համապատասխանաբար

հավասար են մյուսի ներքնաձիգին և էջին, ապա այդ եռանկյունները հավասար են

Թեորեմներ
Պյութագորասի թեորեմ։ Ուղղանկյուն եռանկյան ներքնաձիգի քառակուսին հավասար է էջերիքառակուսիների գումարին՝
a^2 + b^2 = c^2\,։
(Պյութագորասի հակադարձ թեորեմ) Եթե եռանկյան մի կողմի քառակուսին հավասար է մյուսերկու կողմերի քառակուսիների գումարին, ապա այդ եռանկյունը ուղղանկյուն եռանկյուն է:
Կոսինուսների թեորեմ։ Եռանկյան ցանկացած կողմի քառակուսին հավասար է մյուս երկուկողմերի քառակուսիների գումարին՝ հանած այդ կողմերի և նրանցով կազմված անկյանկոսինուսի կրկնապատիկ արտադրյալը՝
c² = a² + b² – 2ab cos γ։
Այն հանդիսանում է Պյութագորասի թեորեմի ընդհանրացված տարբերակը։
Սինուսների թեորեմ։ Եռանկյան կողմերը համեմատական են հանդիպակաց անկյուններիսինուսներին՝

Հավասարասրուն եռանկյուն

Եռանկյունը կոչվում է հավասարասրուն, եթե նրա երկու կողմերը հավասար են:

Հավասար կողմերը կոչվում են սրունքներ, երրորդ կողմը` հիմք:

 Հավասարասրուն եռանկյան հիմքին առընթեր անկյունները հավասար են:

 Եթե հավասարասրուն եռանկյան անկյուններից որևէ մեկը 60° է, ապա այդ եռանկյունը

հավասարակողմ եռանկյուն է:

 Հավասարասրուն եռանկյան հիմքին տարված բարձրությունը, կիսորդն ու միջնագիծը համընկնում են:

 Եթե եռանկյան երկու անկյունները հավասար են, ապա եռանկյունը հավասարասրուն է:

Հավասարակողմ եռանկյուն

Եռանկյունը, որի բոլոր կողմերը հավասար են կոչվում է հավասարակողմ կամ

կանոնավոր եռանկյուն:

Հավասարակողմ եռանկյան անկյունները 60° են:

 Հավասարակողմ եռանկյան նույն կողմին տարված միջնագիծը, կիսորդն ու

բարձրությունը համընկնում են:

Հավասարակողմ եռանկյան մակերեսը կարելի է հաշվել

Սուրանկյուն եռանկյուն

Եռանկյունը, որի բոլոր անկյունները սուր են, կոչվում է սուրանկյուն եռանկյուն:

 Եթե եռանկյան ամենամեծ կողմի քառակուսին փոքր է մյուս կողմերի քառա-

կուսիների գումարից, ապա այն սուրանկյուն եռանկյուն է:

Բութանկյուն եռանկյուն

Եռանկյունը, որի անկյուններից մեկը բութ է կոչվում է բութանկյուն եռանկյուն:

 Եթե եռանկյան ամենամեծ կողմի քառակուսին մեծ է մյուս կողմերի

քառակուսիների գումարից, ապա այն բութանկյուն եռանկյուն է:

 Նման եռանկյուններ

Այն եռանկյունները, որոնց անկյունները համապատասխանաբար հավասար են,

իսկ կողմերը` համեմատական, կոչվում են նման եռանկյուններ: 

Եթե մի եռանկյան երկու անկյունները համապատասխանաբար հավասար են

մյուսի երկու անկյուններին, ապա այդպիսի եռանկյունները նման են:

Եթե մի եռանկյան երկու կողմերը համեմատական են մյուսի երկու կողմերին, և

այդ կողմերով կազմված անկյունները հավասար են, ապա այդպիսի եռանկյուն-

ները նման են:

Եթե մի եռանկյան երեք կողմերը համեմատական են մյուսի երեք կողմերին, ապա

այդպիսի եռանկյունները նման են:

Կիսորդ

Եռանկյան գագաթից տարված կիսորդ է կոչվում եռանկյան անկյան կիսորդի այն հատվածը, որի միացնում է այդ գագաթը և նրա դիմացի կողմի վրա գտնվող կետը։

Եռանկյան կիսորդը հանդիպակաց կողմը բաժանում է երկու մասերի նույն հարաբերությամբ, ինչ որ անկյանը կից կողմերի հարաբերությունն է։

Եռանկյան ներքին անկյունների կիսորդնեը հատվում են մեկ կետում, որը համընկնում է այդ եռանկյանը ներգծած շրջանագծի կենտրոնի հետ։

Եթե եռանկյան երկու կիսորդները հավասար են մեկը մյուսին, ապա այդ եռանկյունը հավասրասրուն է:

Եռանկյան բարձրություն

Եռանկյան գագաթից հանդիպակաց կողմն ընդգրկող ուղղին տարված ուղղա-

հայացը կոչվում է եռանկյան բարձրություն:

Եռանկյան միջինագիծ

Եռանկյան գագաթը հանդիպաց կողմի միջնակետին միացնող հատվածը կոչվում

է եռանկյան միջնագիծ:

 Եռանկյան միջնագծերը հատվում են մի կետում, որը յուրաքանչյուր միջնագիծը բաժանում է2:1 հարաբերությամբ, հաշված գագաթից:

Եռանկյունն իր միջնագծով բաժանվում է երկու հավասարամեծ եռանկյունների:

Եռանկյան միջին գիծ

Եռանկյան միջին գիծ է կոչվում նրա երկու կողմերի միջնակետերը միացնող

հատվածը:

Եռանկյան միջին գիծը զուգահեռ է նրա կողմերից մեկին և հավասար է այդ կողմի

կեսին: